Fyzikální hlavolamy s obrázkem

Květina v zrcadle

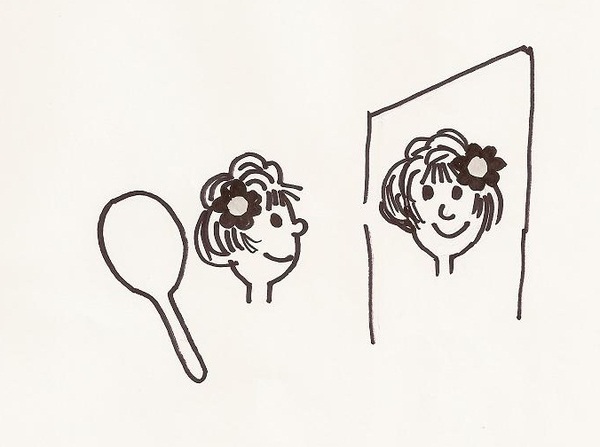
Žena stojí 2 m od velkého zrcadla zavěšeného na stěně a drží malé zrcátko půl metru za hlavou. Jak daleko za velkým zrcadlem je obraz květiny, kterou má ve vlasech.

Řešení: 3 m ( Obraz květiny v malém zrcátku je tak daleko za zrcátkem, jak daleko je květ před ním – 0,5 m. Obraz květiny je 0,5 + 0,5 + 2 = 3 m před velkým zrcadlem. Obraz květiny tedy bude 3 m za velkým zrcadlem.)

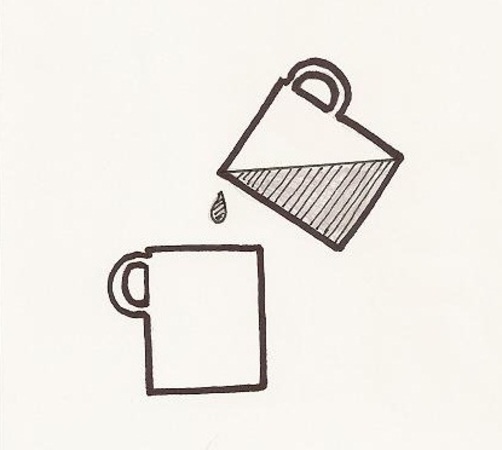
Polovina hrníčku

Vymysli způsob, jak odlít přesně polovinu hrníčku čaje plného až po okraj.

Řešení:

Balancovací plošina

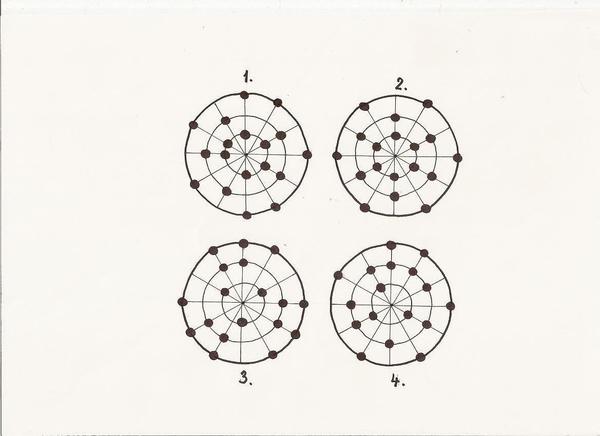
Představ si, že 4 obrázky před tebou jsou kruhové balancovací plošiny a černé body na nich jsou lidé stejné hmotnosti rozmístěné na plošině. Dokážeš určit, které plošiny jsou v rovnováze.

Řešení: Balancovací plošina č. 2 a 3

Rovnováha závaží

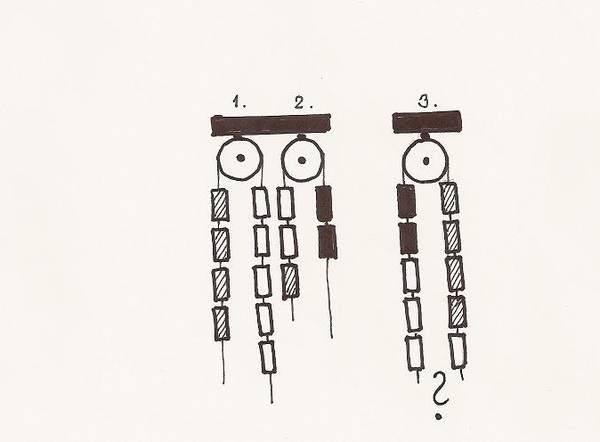
Tři různé druhy závaží jsou uspořádány na dvou kladkách tak, že jsou v rovnováze. Stejné druhy závaží jsou využity i při zavěšení na třetí kladce. Jsou závaží na této kladce v rovnováze?

Řešení: Levá strana je těžší o rozdíl mezi jedním vyšrafovaným a jedním bílým závažím..

Zrcadlové bludiště

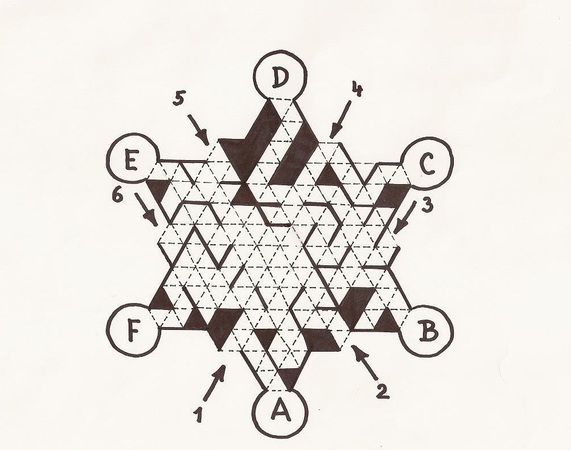
Do bludiště vede 6 vchodů označených šipkami a čísly. V bludišti jsou rozmístěna zrcadla. Pustíme-li určitým vchodem světelný paprsek, dorazí vždy do jedné komůrky označené písmenem. Urči, který vchod patří ke které komůrce.

Řešení: 1E, 2F, 3C, 4B, 5A, 6D

Kde vzít pevný bod

Na náměstí stojí stará věž. Vzniklo podezření, že se věž propadá. Na radnici zasedla komise, která měla najít řešení. Ta rozhodla, že je potřeba najít nějaký nepohyblivý bod, vůči kterému by se zjistilo, zda věž klesá. Ale kde takový bod vzít? Co když se propadá celé náměstí i sousední domy. Ve vzdálenosti 400 m od náměstí je park. A tam jsou skály, které určitě neklesají, ale z těchto skal není vidět na věž, je zakryta velkými domy. Pomůžeš komisi vyřešit tuto složitou situaci?

Řešení: Použijeme dlouhou hadicovou vodováhu

Speciální periskop

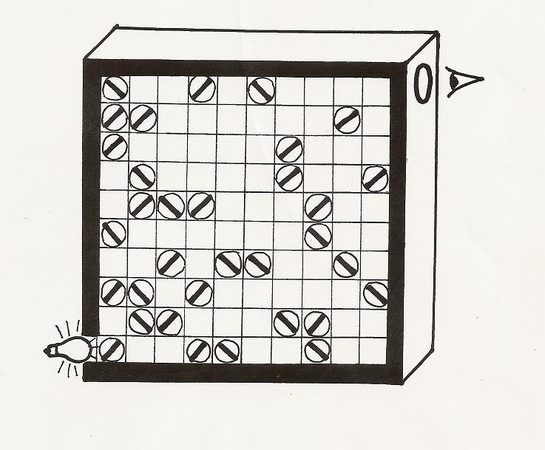
Na obrázku je zařízení, ve které jsou rozmístěna oboustranná zrcadla, kterými můžeme otáčet o 90o . Dokážeš určit, kterými zrcadly je třeba pohnout, abychom v pravém horním rohu viděli obraz žárovky.

Čokoládové bonbóny

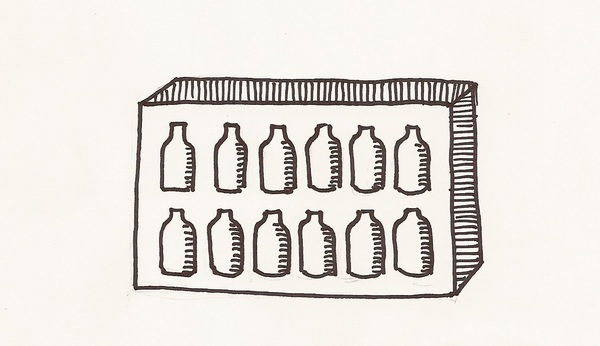
Veronika dostala k narozeninám krabici čokoládových bonbónů. Měly tvar lahviček a byly naplněny hustým malinovým sirupem. Veronice bonbóny chutnaly a také se jí líbil tvar lahviček. Proto začala s kamarády přemýšlet, jak se vyrábějí. Jeden kamarádů navrhl: „Nejdříve se vyrobí čokoládové lahvičky a potom se plní sirupem. Přitom sirup musí být hustý, aby se bonbón nerozpustil.“ Ale hustý sirup nelze snadno a rychle nalít do lahvičky. Pomohlo by, kdybychom sirup nahřáli, aby byl tekutější. Horký sirup však roztaví čokoládovou lahvičku. Jak bys vyrobil čokoládové bonbóny ty?

Řešení: Sirup nalijeme do formy a zmrazíme. Zmrzlé sirupové lahvičky pak ponoříme do roztavené čokolády.

Co je uvnitř krabice

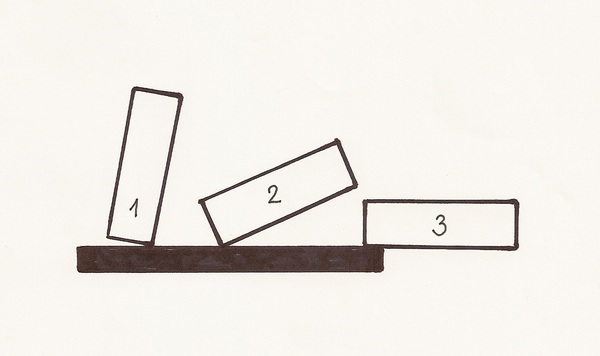
Na obrázcích je znázorněna krabice ve třech polohách. Když je krabice v poloze 1, stačí do ní jen trochu strčit a krabice se převrátí. Když je v poloze 2, můžeme do ní strkat až do zobrazeného náklonu, než se převrátí. V poloze 3, i když většina krabice přečnívá, je krabice v rovnovážné poloze.

Řešení:

Jaký je objem láhve?

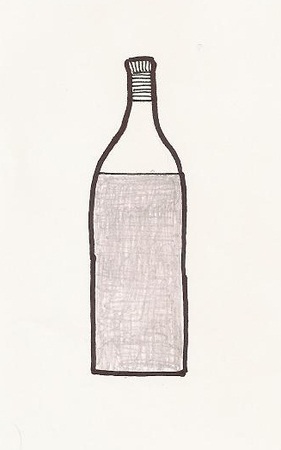
Uzavřená válcová láhev je částečně naplněna vínem. (Víno nepřesahuje nad zakřivenou část láhve.) Máš jen pravítko a kalkulačku. Dovedeš určit objem celé láhve, aniž bys ji otevřel?

Řešení: Nejdříve změř průměr dna láhve. Urči z něj poloměr a vypočítej obsah kruhového dna. Pak změř výšku vína. Láhev otoč dnem vzhůru a změř výšku vzduchu. Objem celé láhve je „válec vína +válec vzduchu. Proto sečti obě změřené výšky a výsledek vynásob obsahem dna. Dostaneš objem celé láhve.

„U“ trubice

Vodu nalijeme do průhledné U trubice, Výška vody v obou ramenech je stejná. Pak dejte palec k jednomu konci trubice a opatrně ji naklánějte, dokud se voda nedotkne palce. Pak palec pevně přitiskni ke konci trubice. Když vrátíme trubici do původní polohy, voda se bude stále dotýkat prstu. Dokážeš vysvětlit, co způsobilo, že jsou rozdílné hladiny vody v ramenech trubice?

Řešení: Palec zabraňuje vzduchu dostat se k hladině na tomto konci trubice. Vzduch však tlačí na vodu v otevřeném konci trubice a drží vodu v dané poloze.

Prst ve sklenici

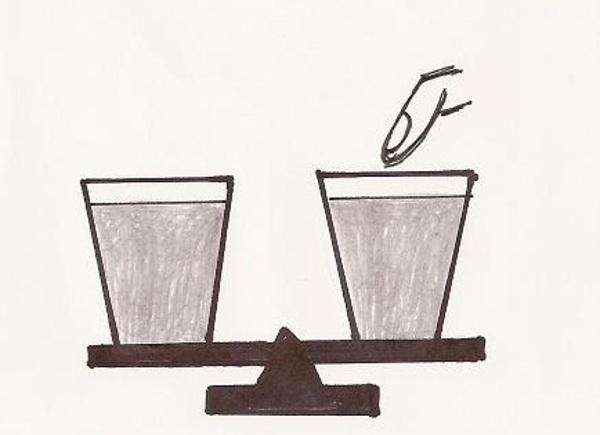
Dvě sklenice naplněné vodou jsou vyváženy na váze. Co se stane, když do jedné sklenice strčíš prst? Jak se změní výsledek, když bude tvůj prst z těžkého kovu?

Řešení: Když strčíš do vody prst, vytlačí určitý objem vody a její hladina tedy stoupne. Tvůj prst zabral místo části vody a také zastoupí její hmotnost. Sklenice váží o tolik víc, jaká je hmotnost vytlačené vody. Přitom tato situace nezávisí na látce, ze které je „ponořený prst“, ale jen na objemu ponořené části.

Nádrž

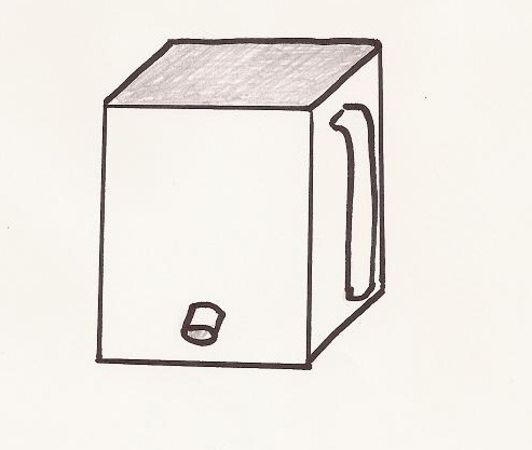
Nádrž má 2 stejné otvory určené k vypouštění vody. Jeden otvor je u dna nádoby, druhý je na konci trubice, která je napojená blízko na vrchu nádoby, ale ústí na jedné úrovni jako první otvor. Dokážeš určit, kterým otvorem vytéká voda rychleji (komplikující faktory, např. tření zanedbáváme).

Řešení: Rychlost vytékající vody závisí na tom, jak nízko pod úrovní hladiny je otvor, kterým voda vytéká. Hladina je pro oba dva otvory stejná, takže voda poteče z obou otvorů stejně rychle.

Nádrže s různými otvory

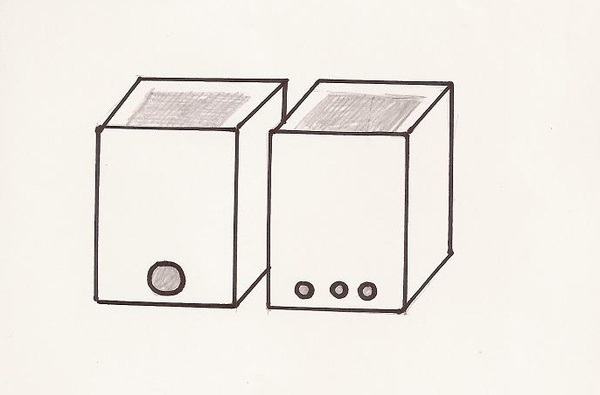
Máme 2 stejné nádrže, liší se jen počtem a velikostí otvorů, kterými vytéká voda. První nádrž má jen jeden otvor o průměru 6 cm, druhá má 3 vypouštěcí otvory, každý o průměru 2 cm. Dokážeš určit, která nádrž se vyprázdní jako první, otevřeme-li všechny otvory najednou.

Řešení: Otvor s průměrem 6 cm má 3x větší obsah než všechny 3 menší otvory dohromady, takže se první nádrž s větším otvorem vypustí rychleji..

Co nejméně závaží

Na rovnoramenných vahách máme zvážit libovolnou hmotnost od 1 do 40 g (jen celé gramy). Urči nejmenší počet závaží, které k tomu potřebuješ.

Řešení: Stačí závaží: 1g, 2g, 4g, 8g,16g, 32g. (Pokud by mohla být závaží na obou miskách, stačí závaží 1g, 3g, 9g, 27g.)